Nernst Equation

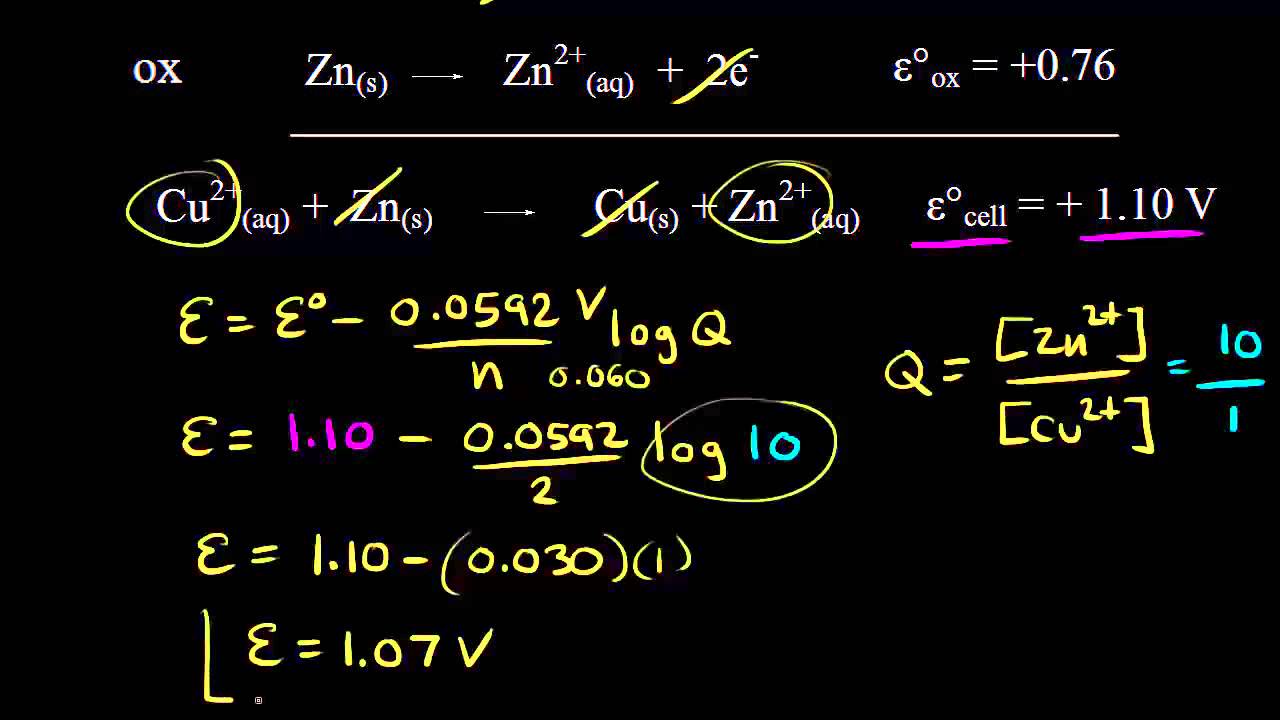
Source: YouTube

The Nernst Equation and Electrochemical Potential

When it comes to redox reactions, the standard electrochemical potential plays a crucial role in determining the voltage. Under standard conditions, the voltage is defined as the potential difference between the redox reaction components in a solution (1 molar for aqueous solutions) or gases (1 atmosphere). However, this voltage can vary based on the concentration of components in the reaction mixture or the pressure of gaseous reactants.

The Nernst equation provides a way to calculate the voltage under non-standard conditions:

E = E 0 – (R * T * n * F) * ln(Q)

Here, R is the universal gas constant, T is the temperature, F is Faraday’s constant, n is the number of moles of electrons exchanged in the reaction, and Q is the reaction quotient that depends on the concentrations or pressures of the reactants.

Understanding the Components of the Nernst Equation

The Nernst equation takes into account the impact of concentration changes on the voltage of a redox reaction. For reactions involving liquids or gases, changes in concentration or pressure can alter the average energy of the components, leading to variations in voltage.

For reactions involving solids, the concentration term in the equation simplifies to 1, indicating that the voltage remains constant as solid components do not change their concentration. This is particularly relevant for battery systems with all solid components, where the voltage does not depend on concentration changes.

Implications for Battery Systems

One significant implication of the Nernst equation is its effect on battery performance. In batteries with components that can change concentration, such as lead-acid batteries, the voltage fluctuates during charging and discharging processes due to concentration variations in the electrolyte.

On the other hand, batteries composed entirely of solid components exhibit a consistent voltage as their concentrations remain constant. This stability in voltage is essential for certain types of battery technologies where maintaining a constant voltage is critical for optimal performance.

Source: YouTube