Basic Equations

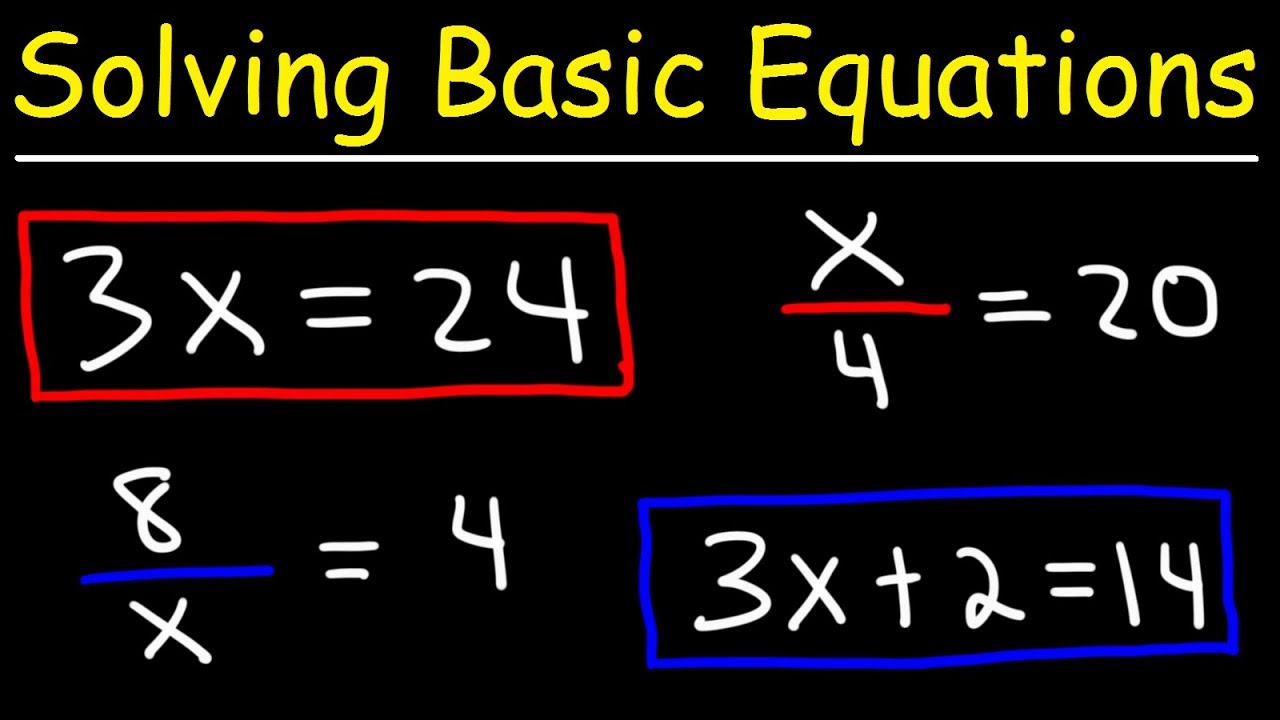
Source: YouTube

Poisson’s Equation

The Poisson’s Equation relates the electric field (E) to the charge density (ρ) and material permittivity (ε). It expresses the fundamental connection between charge and electric field strength in a given medium. In semiconductors, the charge is divided into hole density (p), electron density (n), acceptor atom density (N_A), and donor atom density (N_D).

Transport Equations

The Transport Equations describe the movement of carriers in a semiconductor. They include the electron current density (J_n), electron mobility (μ_n), electron diffusivity (D_n), hole current density (J_p), hole mobility (μ_p), hole diffusivity (D_{p>), electronic charge (q), and electric field (E). These equations account for both drift and diffusion of carriers.}

Continuity Equations

The Continuity Equations track the movement, generation, and recombination of carriers in a semiconductor. They ensure that all carriers are properly taken into consideration, acting as ‘book keeping’ equations for carriers.

General Conditions

The General Conditions equations involve the rates of carrier recombination (U) and generation (G) in the semiconductor. These equations help in understanding the behavior of carriers over time in the material.

Summary

In summary, the set of equations including Poisson’s Equation, Transport Equations, Continuity Equations, and General Conditions provide a comprehensive framework for analyzing carrier behavior in semiconductors. These equations can be solved using numerical methods or device simulators to study the performance of semiconductor devices.

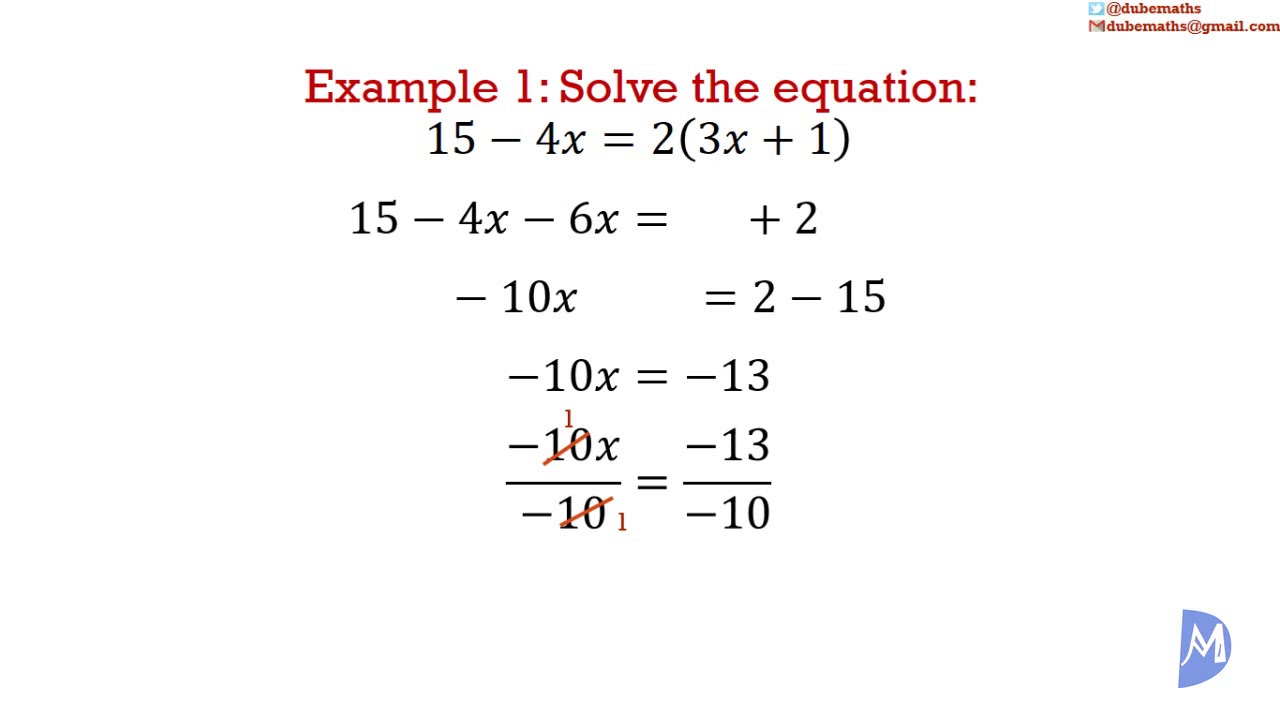
Source: YouTube

Feel free to comment your thoughts.